PDF um HELP na Prova

Clique na imagem e abra o PDF.

Dias não letivos

Recebemos o seguinte e-mail de nosso representante de sala:

A Reitora do Centro Universitário das Faculdades Metropolitanas Unidas, no uso de suas atribuições, nos termos do art. 12, item I, 4, do Regimento,

 

Resolve:

Alterar o  Calendário Escolar, considerando não letivo os dias 16, 18 e 19 de novembro de 2013, em virtude dos feriados da Proclamação da República e da Consciência Negra.

Atenciosamente,

Profa. Ms. Angela Tomiko Ninomia

FMU - Coordenadora de Curso

 

Atividades Complementares

Clique na imagem a baixo e veja a noticia!

Sequência de Fibonacci

O matemático Leonardo Pisa, conhecido como Fibonacci, propôs no século XIII, a sequência numérica abaixo:

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...)

Essa sequência tem uma lei de formação simples: cada elemento, a partir do terceiro, é obtido somando-se os dois anteriores. Veja: 1+1=2, 2+1=3, 3+2=5 e assim por diante.

Desde o século XIII, muitos matemáticos, além do próprio Fibonacci, dedicaram-se ao estudo da seqüência que foi proposta, e foram encontradas inúmeras aplicações para ela no desenvolvimento de modelos explicativos de fenômenos naturais.

Veja algumas exemplos das aplicação da seqüência de Fibonacci e entenda por que ela é conhecida como uma das maravilhas da Matemática.

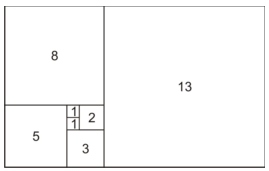
A partir de dois quadrados de lado 1, podemos obter um retângulo de lados 2 e 1. se adicionarmos a esse retângulo um quadrado de lado 2, obtemos um novo retângulo 3x2. Se adicionarmos agora um quadrado de lado 3, obtemos um retângulo 5x3. Observe a figura a seguir e veja que os lados dos quadrados que adicionamos para determinar os retângulos formam a sequência de Fibonacci.

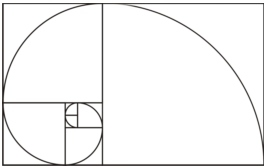
Se utilizarmos um compasso e traçarmos o quarto de circunferência inscrito em cada quadrado, encontraremos uma espiral formada pela concordância de arcos cujos raios são os elemento da seqüência de Fibonacci.

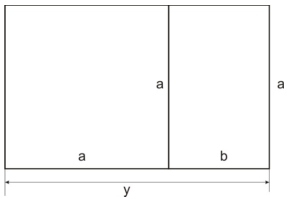
O Partenon  que foi construído em Atenas pelo celebre arquiteto grego Fidias. A fachada principal do edifício, hoje em ruínas, era um retângulo que continha um quadrado de lado igual à altura. Essa forma sempre foi considerada satisfatória do ponto de vista estético por suas proporções sendo chamada retângulo áureo ou retângulo de ouro.

Como os dois retângulos indicados na figura são semelhantes temos:

Como:

Subtituindo (2) em (1) temos:

Resolvendo a equação:

Logo:

Esse número é conhecido como número de ouro e pode ser representado por:

Todo retângulo em que a razão entre o maior e o menor lado for igual a Φ é chamado retângulo áureo como o caso da fachada do Partenon.